Weighted random sampling with replacement,中文翻译为带权重的有放回地采样,简单来说就是每一个样本都有一个权重,然后根据样本权重大小有放回地采样数据,样本的权重越大,样本被选择的概率也就越大。该问题换种方式描述就是,给定一个权重数组 $w$,大小为 $N$,然后根据权重大小,在下标数组 ${0, 1, \ldots, N-1}$ 中进行有放回地采样,下标 $i$ 被选中的概率为 $w[i]/\text{sum}(w)$。
这个采样方法一个应用是在Boosting算法中,Boosting算法每次训练完模型时,根据模型分类的情况改变数据样本的权重,然后用带权重的样本训练下一个模型,如果模型的训练不支持带权重的样本,则进行带权重的样本采样。
本文主要将博文 WEIGHTED RANDOM SAMPLING WITH REPLACEMENT WITH DYNAMIC WEIGHTS 内容进行解析 (文章拷贝:Copy)。算法实现代码在:adefazio/sampler
Rejection Sampling
这个思想很简单,给定一个权重数组 $w \in R^N$,权重最大值为 $w_\max$,然后在下标数组 ${ 0, 1, \ldots, N-1 }$ 中随机采样得到下标 $i$,接下来就是判断该下标是否被accept,首先根据分布 $X \sim U(0, 1)$ 获得一个随机数 $x$,然后判断 $w_\max * x \le w[i]$,如果符合该条件,则accept该下标 $i$,否则就reject该下标。
算法实现的代码如下:
1
2
3
4
5
6
7
8
9
10
| w = [1,4,2,5] # Some data
w_max = max(w)
n = len(w)
while True:
idx = random.randrange(n)
u = w_max*random.random()
if u <= w[idx]:
break
print idx
|
算法思想可以用下面图表示:
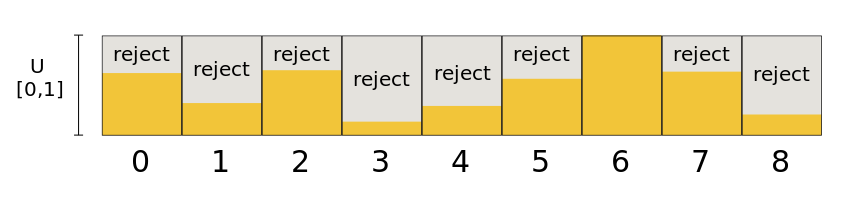
橘色区域代表accept区域,灰色区域代表reject区域。这个算法有个缺点就是当数据不平衡时,性能会很低,因为如果小部分数据权重很大时,$w_\max$ 会变的很大,数据权重小的下标很难被accept,而且权重小的占大部分,这导致算法会经过很多次循环。
Level Rejection Sampling
这个是在Rejection Sampling之前对下标进行分层 (level),根据权重 $w[i]$ 的大小将下标 $i$ 分到不同层中,第 $k$ 层权重的范围为 $[2^k, 2^{k+1}]$,由于每一层内的权重的差距不会偏大,对该层进行Rejection Sampling效率会较高。
该方法的思想如下图所示:
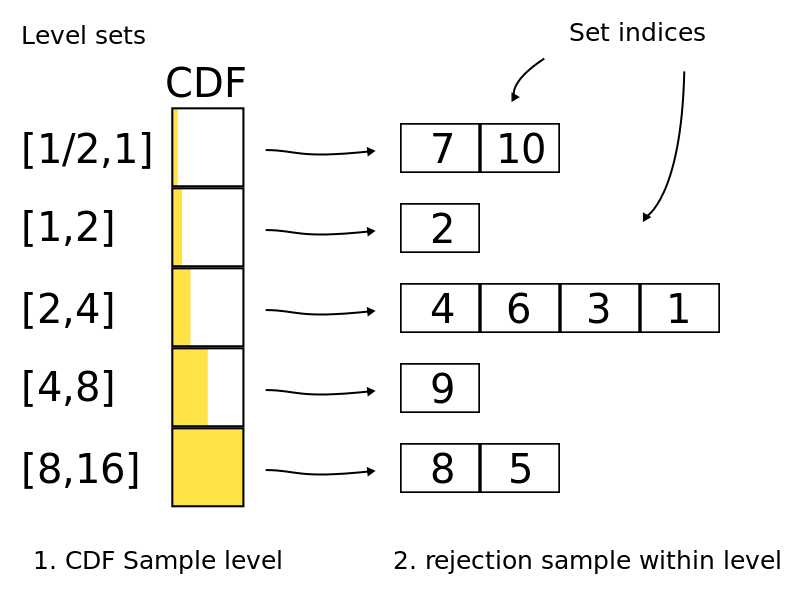
如图所示,总共分了5层,每一层存储的是数组下标。下标分层后,在进行采样时,首先随机选择某一层,然后进行Rejection Sampling获得最终想要的下标。
模拟实验
贴出一段实验代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| import numpy as np
from sampler import Sampler
import matplotlib.pyplot as plt
if __name__ == '__main__':
weights = np.array([1, 1, 3, 5, 2], dtype='d')
num_entries = len(weights)
normalized_weights = weights / np.sum(weights)
weight_sampler = Sampler(num_entries, max_value=100, min_value=1)
for i in range(num_entries):
weight_sampler.add(i, weights[i])
num_samples = 10000
distro = np.zeros(num_entries)
for i in range(num_samples):
idx = weight_sampler.sample()
distro[idx] += 1
normalized_distro = distro / np.sum(distro)
print('Sample distribution: {}'.format(distro))
print('Weights distribution: {}'.format(weights))
print('Normalized sample distribution: {}'.format(normalized_distro))
print('Normalized weights distribution: {}'.format(normalized_weights))
plt.bar(np.arange(num_entries),
normalized_weights, width=0.35,
label='Normalized Weights Distribution')
plt.bar(np.arange(num_entries)+0.35,
normalized_distro, width=0.35,
label='Normalized Sample Distribution')
plt.legend()
plt.show()
|
输出为:
1
2
3
4
| Sample distribution: [ 843. 824. 2513. 4182. 1638.]
Weights distribution: [1. 1. 3. 5. 2.]
Normalized sample distribution: [0.0843 0.0824 0.2513 0.4182 0.1638]
Normalized weights distribution: [0.08333333 0.08333333 0.25 0.41666667 0.16666667]
|
得到的结果如下图所示:
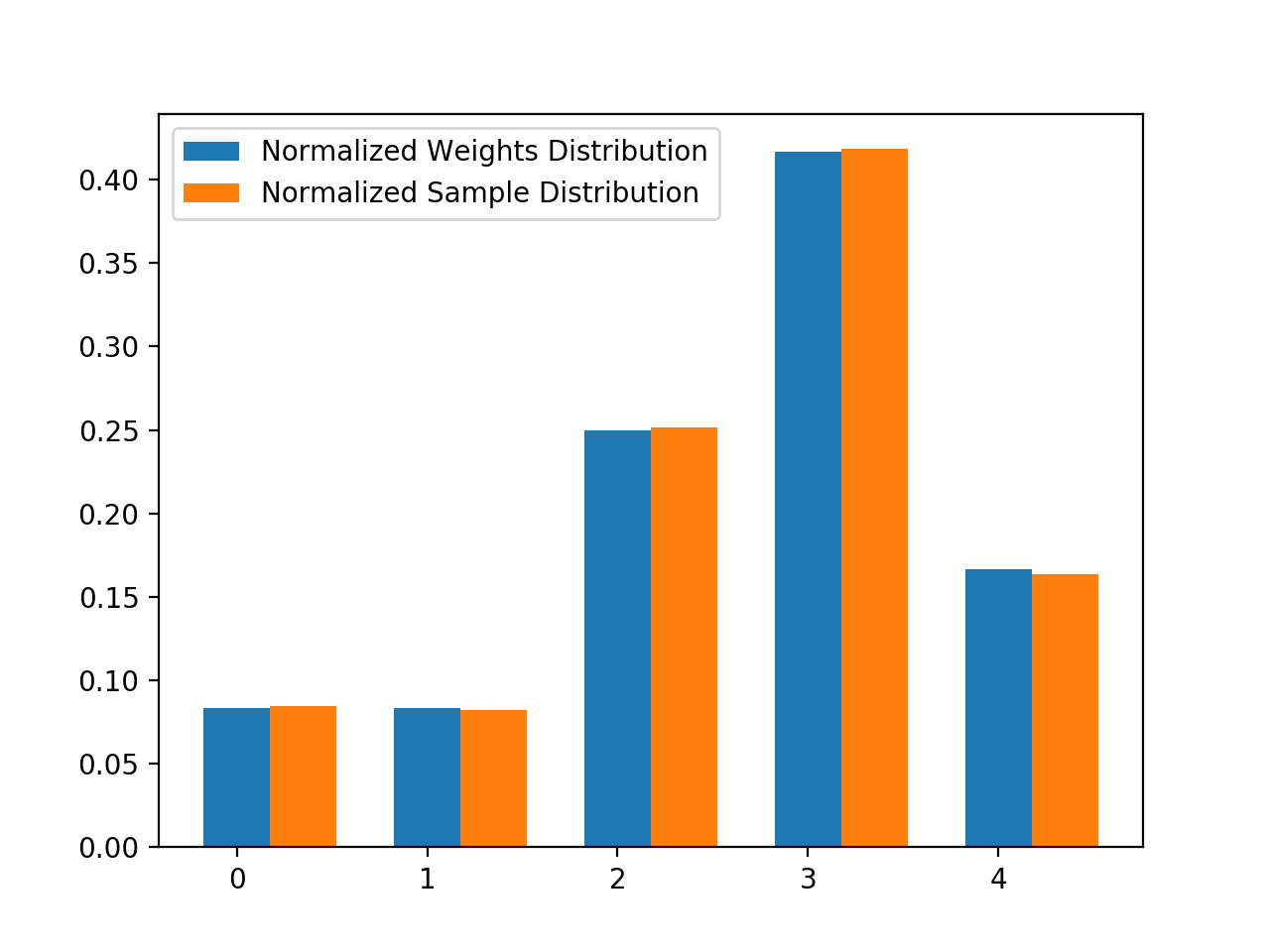
图中横坐标代表数组下标,蓝色柱代表各个下标的权重大小 (归一化),橘色柱代表经过大量采样时,各个下标被采中的比例。从图中可以看出,采样结果基本符合权重分布规律,权重越大,被采中的概率也就越大。


