袋熊的树洞

日拱一卒，功不唐捐

0%

Posted on Edited on

问题描述

Given a string, you need to reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.

Example 1:

1
2
Input: "Let's take LeetCode contest"
Output: "s'teL ekat edoCteeL tsetnoc"

Note: In the string, each word is separated by single space and there will not be any extra space in the string.

Related Topics: String

原问题：557. Reverse Words in a String III

解决方案

题目主要意思是反转字符串中的每一个单词，因此这道题目主要是找到单词的位置，这里我们可以设定两个指针，分别命名为start和end，指针start指向单词的第一个字母的位置，指针end指向单词的最后一个字母的位置，然后将[start, end]里面的单词反转即可。至于指针怎么设置，我们可以先设置指针start指向第一个字母，然后找到空格字符的前一个字符的位置赋给指针end；接着找到下一个字母的位置赋给指针start，然后找到下一个空格字符的位置，将该空格字符的前一个字符的位置赋给指针end，如此循环，直到字符串被遍历完。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <string>
using namespace std;

class Solution {
public:
    string reverseWords(string s)
    {
        int start, end;
        char tmp;

        start = 0;
        end = s.size();
        for (int i=0; i<s.size(); i++) {
            if (s[i] == ' ') {
                end = i - 1;

                // reverse word
                while (start < end) {
                    tmp = s[start];
                    s[start] = s[end];
                    s[end] = tmp;
                    start++;
                    end--;
                }

                while (i < s.size() && s[i] == ' ')
                    i++;
                start = i;
            }
        }

        // process last word
        end = s.size() - 1;
        while (start < end) {
            tmp = s[start];
            s[start] = s[end];
            s[end] = tmp;
            start++;
            end--;
        }

        return s;
    }
};

int main()
{
    Solution solu;
    string str1 = "Let's take LeetCode contest";

    cout << str1 << endl;
    cout << solu.reverseWords(str1) << endl;

    return 0;
}

Posted on Edited on

介绍

本文主要介绍如何利用Docker搭建Caffe的开发环境，内容分两部分，第一部分是CPU模式环境搭建，第二部分是GPU模式环境搭建。

准备工作

由于本文需要用到Docker的，所以要先装好Docker，这个教程可以参考官方提供的最新教程 Install Docker，这里就不详细介绍了。按照官方教程，装好Docker的社区版 (Community Edition)。

CPU模式

如果要想直接使用Caffe提供的Docker镜像 (bvlc/caffe)，可以直接使用 docker pull 命令把镜像下下来，然后使用 docker run 运行一个容器。

1
2
docker pull bvlc/caffe:cpu
docker run -it bvlc/caffe:cpu bash

此时，CPU模式的环境就可以使用了。如果需要在这个镜像的基础上添加点东西，例如安装 Jupyter Notebook 从而方便地使用Caffe的Python接口，这就需要自己编写一个Dockerfile了，然后生成一个镜像。

编写Dockerfile

我这里直接贴上一份Dockerfile，内容如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
FROM bvlc/caffe:cpu

RUN pip install -U pip \
    && pip install -U scipy \
    && pip install -U scikit-learn \
    && pip install -U matplotlib \
    && pip install -U jupyter \
    && pip install -U lmdb \
    && pip install -U python-mnist

# Set the working directory to /caffe
WORKDIR /caffe

VOLUME ["/caffe/data", "/caffe/notebooks"]

# Expose port 8888 (jupyter uses)
EXPOSE 8888

CMD jupyter notebook --no-browser --ip=0.0.0.0 --allow-root --NotebookApp.token='science'

关于Dockerfile的编写规则，可以参考Docker - 从入门到实践这个电子书，内容写的很不错。Dockerfile选择Caffe作为基础镜像，然后安装了一些Python 包。在这个Dockerfile中我使用 VOLUME 命令定义了两个匿名卷

1
VOLUME ["/caffe/data", "/caffe/notebooks"]

后面我会把主机的真实目录挂载为这两个匿名卷，这样你在容器里往这两个目录写入东西就会保存到主机的真实目录里面。Dockerfile还指定了容器启动命令

1
CMD jupyter notebook --no-browser --ip=0.0.0.0 --allow-root --NotebookApp.token='science'

每次使用 Docker run 启动容器都会运行这个命令，这里我选择启动 Jupyter Notebook，这样我就可以通过浏览器访问 Jupyter Notebook了。

制作镜像

在Dockerfile所在目录使用命令即可

1
docker build -t mycaffe .

启动容器

创建两个目录，分别为 data 和 notebooks

1
2
mkdir data
mkdir notebooks

这两个目录就是所要挂载的目录，我要将这两个目录挂载到容器的匿名卷上。使用 Docker run 启动一个容器

1
docker run --name DeepLearning -d --mount type=bind,source=`pwd`/data,target=/caffe/data --mount type=bind,source=`pwd`/LeNet,target=/caffe/notebooks -p 8887:8888 mycaffe

这里解析下命令，首先是挂载两个匿名卷，将目录 data 挂载到 /caffe/data，将目录 notebooks 挂载到 /caffe/notebooks

1
--mount type=bind,source=`pwd`/data,target=/caffe/data --mount type=bind,source=`pwd`/LeNet,target=/caffe/notebooks

然后是 -p 8887:8888 将容器8888端口映射到本机的8887端口上，-d 是让容器后台运行，--name DeepLearning 将这个容器命名为 DeepLearning。运行成功后，可以使用浏览器访问 Jupyter Notebook了，访问地址为：

1
http://localhost:8887/

GPU模式

GPU模式稍微复杂点，主要是GPU模式下需要CUDA以及显卡驱动，不过Caffe镜像已经集成了相应的CUDA，剩下就是安装显卡对应的驱动了。不同于CPU模式，这里启动容器需要使用 nvidia-docker，具体安装可以参考 GitHub Nvida Docker，安装过程很简单，很快就可以安装好了。接下来就需要编写Dockerfile了，大体内容类似CPU模式的Dockerfile，不过基础镜像选择 bvlc/caffe:gpu。

编写Dockerfile

选用 bvlc/caffe:gpu 作为基础镜像，编写Dockerfile如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
FROM bvlc/caffe:gpu

RUN pip install -U pip \
    && pip install -U scipy \
    && pip install -U scikit-learn \
    && pip install -U matplotlib \
    && pip install -U jupyter \
    && pip install -U lmdb \
    && pip install -U python-mnist

# Set the working directory to /caffe
WORKDIR /caffe

VOLUME ["/caffe/data", "/caffe/notebooks"]

# Expose port 8888 (jupyter uses)
EXPOSE 8888

CMD jupyter notebook --no-browser --ip=0.0.0.0 --allow-root --NotebookApp.token='science'

制作镜像

在Dockerfile所在目录执行命令

1
docker build -t mycaffe .

启动容器

同前面所述，先创建好两个目录

1
2
mkdir data
mkdir notebooks

然后启动容器，启动容器使用的是 nvidia-docker 而不是 docker，启动命令如下

1
nvidia-docker run --name DeepLearning -d --mount type=bind,source=`pwd`/data,target=/caffe/data --mount type=bind,source=`pwd`/LeNet,target=/caffe/notebooks -p 8887:8888 mycaffe

启动完后可以直接通过浏览器访问容器内部的 Jupyter Notebook 了。

参考

  1. Docker Setup Cafee

Posted on Edited on

源码

源码以及相对应的使用在：GitHub

利用Matplotlib可视化决策树，代码来源于《机器学习实战》，原始的Python代码使用了一些函数属性来实现属性全局共享，这里用全局变量替换了函数属性，并且支持中文标注，修改后的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
"""
Decision Tree Plotter
Reference:
    1. http://www.cnblogs.com/fantasy01/p/4595902.html
    2. http://whatbeg.com/2016/04/23/matplotlib-desiciontree.html
"""

import matplotlib.font_manager as font_manager
import os
import matplotlib.pyplot as plt


# Chinese font setting
font_path = os.path.abspath('../resources/font/msyh.ttf')
prop = font_manager.FontProperties(fname=font_path)

gAxis = None
gDecison_node = dict(boxstyle='sawtooth', fc='0.8')
gLeaf_node = dict(boxstyle='round4', fc="0.8")
gArrow_args = dict(arrowstyle='<-')
gNum_leaves = 0
gTree_depth = 0
gX_offset = 0
gY_offset = 0


def get_num_leafs(tree):
    """
    Identify the number of leaves in a tree
    """
    num_leafs = 0
    first_str = list(tree.keys())[0]
    second_dict = tree[first_str]
    for key in second_dict.keys():
        if isinstance(second_dict[key], dict):
            num_leafs += get_num_leafs(second_dict[key])
        else:
            num_leafs += 1

    return num_leafs


def get_tree_depth(tree):
    """
    Identiy the depth of a tree
    """
    max_depth = 0
    first_str = list(tree.keys())[0]
    second_dict = tree[first_str]
    for key in second_dict.keys():
        if isinstance(second_dict[key], dict):
            subtree_depth = 1 + get_tree_depth(second_dict[key])
        else:
            subtree_depth = 1

        if subtree_depth > max_depth:
            max_depth = subtree_depth

    return max_depth


def plot_node(node_text, center_point, parent_point, node_type):
    global gAxis

    gAxis.annotate(node_text, xy=parent_point,
                   xycoords='axes fraction',
                   xytext=center_point,
                   textcoords='axes fraction',
                   va='center', ha='center',
                   bbox=node_type, arrowprops=gArrow_args,
                   fontproperties=prop)


def plot_mid_text(current_point, parent_point, text_str):
    """
    Plot text between child and parent
    """
    global gAxis

    x_mid = (parent_point[0] - current_point[0])/2.0 + current_point[0]
    y_mid = (parent_point[1] - current_point[1])/2.0 + current_point[1]
    gAxis.text(x_mid, y_mid, text_str, fontproperties=prop)


def plot_tree(tree, parent_point, node_text):
    global gAxis, gDecison_node
    global gNum_leaves, gTree_depth, gX_offset, gY_offset

    num_leaves = get_num_leafs(tree)
    first_str = list(tree.keys())[0]
    current_point = (gX_offset+(1.0+float(num_leaves))/(2.0*gNum_leaves),
                     gY_offset)
    plot_mid_text(current_point, parent_point, node_text)
    plot_node(first_str, current_point, parent_point, gDecison_node)
    second_dict = tree[first_str]
    gY_offset = gY_offset - 1.0/gTree_depth
    for key in second_dict.keys():
        if isinstance(second_dict[key], dict):
            plot_tree(second_dict[key], current_point, str(key))
        else:
            gX_offset = gX_offset + 1.0/gNum_leaves
            plot_node(second_dict[key], (gX_offset, gY_offset),
                      current_point, gLeaf_node)
            plot_mid_text((gX_offset, gY_offset), current_point, str(key))
    gY_offset = gY_offset + 1.0/gTree_depth


def create_plot(tree):
    global gAxis, gNum_leaves, gTree_depth, gX_offset, gY_offset

    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    gAxis = plt.subplot(111, frameon=False, **axprops)
    gNum_leaves = float(get_num_leafs(tree))
    gTree_depth = float(get_tree_depth(tree))
    gX_offset = -1/(2.0 * gNum_leaves)
    gY_offset = 1.0
    plot_tree(tree, (0.5, 1.0), '')
    plt.show()

参考

  1. 机器学习实战决策树plotTree函数完全解析
  2. 利用matplotlib画决策树

Posted on Edited on

题目分两大部分，第一部分是不定项选择题，题目有25道，第二部分是问答题，题目有3道。

选择题

问题1

同事小鹅在训练深度学习模型时发现训练集误差不断减少，测试集误差不断增大，以下解决方法错误的是

A. 数据增强

B. 增加网络深度

C. 提前停止训练

D. 添加dropout

问题2

以下关于鞍点上的Hessian矩阵的描述哪个是正确的

A. 正定矩阵

B. 负定矩阵

C. 半正定矩阵

D. 都不对

问题3

在最佳情况下，快速排序的运行时间复杂度是

A. $O(1)$

B. $O(N)$

C. $O(N \log N)$

D. $O(N^2)$

问题4

以下图像为深度神经网络的激活函数的函数图像，最有可能发生梯度消失的是：

A.

B.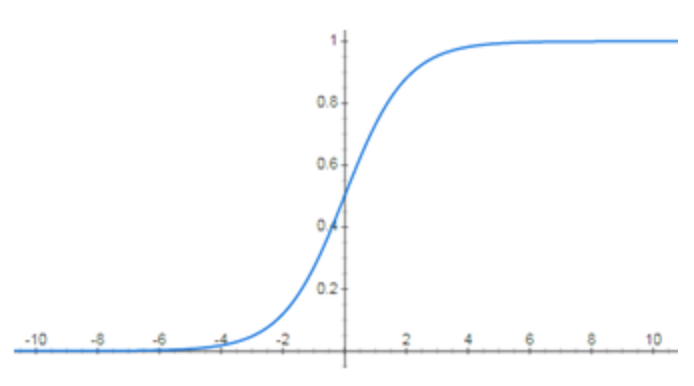

C.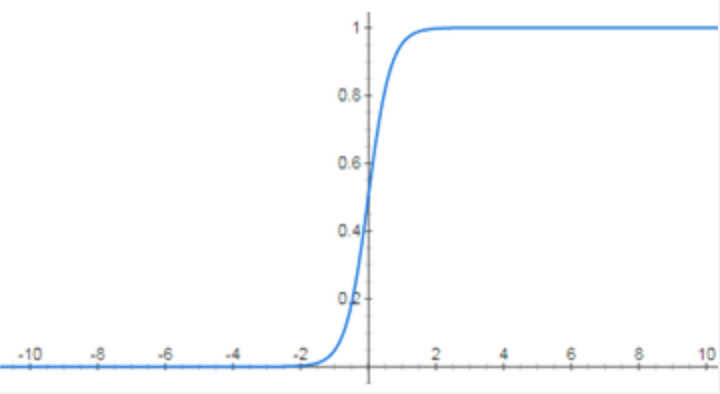

D.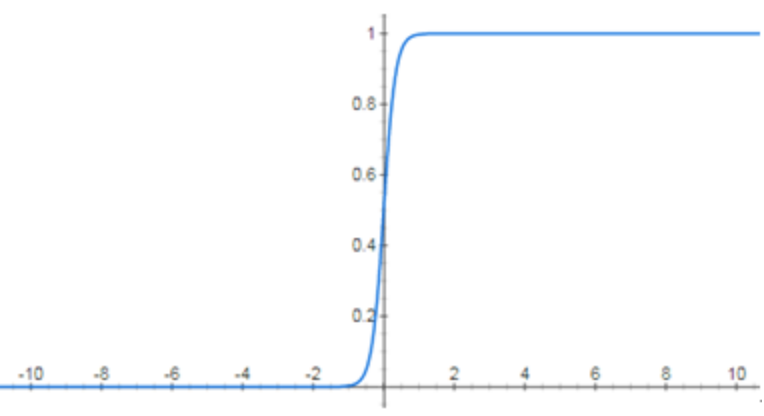

问题5

使用冒泡排序对 [5 7 0 9 2 3 1 4] 进行从小到大排序，一共需要交换多少次

A. 15

B. 16

C. 17

D. 18

问题6

《绝地求生》游戏中，共有1-3三个等级的头盔，1-3三个等级的防弹衣。假设你从无头盔、无防弹衣开始，每次只捡起没有的装备，或将低等级的装备换成高等级的对应装备，那么达到三级头盔、三级防弹衣，总共有多少种方法？ (比如用(x, y)表示当前(头盔，防弹衣)的级别，0为无对应装备，则(0, 0)->(1, 0)->(1, 3)->(3, 3)为一种方法)

A. 6

B. 20

C. 64

D. 106

问题7

以下几种优化方法中，哪种对超参数最不敏感

A. SGD (stochastic gradient descent)

B. BGD (batch gradient descent)

C. Adadelta

D. Momentum

问题8

关于时间复杂度下列说法错误的是

A. 二叉树插入操作的时间复杂度为 $O(\log N)$

B. 堆排序时间复杂度为 $O(N \log N)$

C. 希尔排序时间复杂度为 $O(N^{\frac{7}{5}})$

D. 桶排序最坏情况下时间复杂度为 $O(N^2)$

问题9

设总体 $X$ 在区间 $[-1, 1]$ 上服从均匀分布，已知样本 $X_1, X_2, \ldots, X_n$ 的样本均值 $E(X)$ 和样本方差 $D(X)$，则 $D(\bar{X}) = $

A. $0$

B. $\frac{1}{3}$

C. $\frac{1}{3} n$

D. $3$

问题10

设随机变量 $X$ 满足：$E(X) = \mu$，$D(X) = \sigma^2$，则由切比雪夫不等式，有 $P(\vert X - \mu | \ge 4 \sigma) \le$

A. $\frac{1}{4}$

B. $\frac{1}{2}$

C. $\frac{1}{16}$

D. $\frac{1}{8}$

问题11

对 $n$ 个观测样本点 $(x, y)$ 进行无截距的线性回归拟合，使得残差平方和最小，回归方程为 $y=kx$，则可推导出回归系数 $k$ 为？

A. $k = \frac{\sum_{i=0}^n x_i y_i - n \bar{x} \bar{y}}{\sum_{i=0}^n x_i^2 - n \bar{x}^2}$

B. $k = \frac{\bar{y}}{\bar{x}}$

C. $k = \frac{\sum_{i=0}^n x_i y_i }{\sum_{i=0}^n x_i^2}$

D. 均不正确

问题12

一生产线生产的产品成箱包装，假设每箱平均重50kg，标准差为3kg。若用最大载重量为5000kg的汽车来承运，试用中心极限定理计算每辆车最多装多少箱，才能保证汽车不超载的概率大于0.84 (设 $\Phi(1) =0.84$，其中 $\Phi(x)$ 是标准正太分布 $N(0, 1)$ 的分布函数)

A. 最多装96箱

B. 最多装97箱

C. 最多装98箱

D. 最多装99箱

问题13

分层抽样方法，在下面哪种情况下是比较合适的选择

A. 研究的总体非常小

B. 在调研中希望了解不同子群体的差异

C. 总体中只有一部分样本是可以调研的

D. 没有先验的总体信息

问题14

在无线网络中分别以概率0.6和概率0.4，发出信号”0”和”1”，由于通讯系统受到干扰，当发送”0”时，接收方以概率0.8收到”0”，概率0.2收到”1”，当发送”1”时，接收方以概率0.9收到”1”，概率0.1收到”0”，则下列说法正确的是

(1) 收到信号”0”的概率是0.52

(2) 收到信号”0”时，发出信号也是”0”的概率是12/13

A. (1) 和(2)都错误

B. (1)正确，(2)错误

C. (1)错误，(2)正确

D. (1)和(2)都正确

问题15

已知 $f(x) = 3x^2 + 4x f’(x)$，则 $f’(0) =$

A. -8

B. -16

C. -24

D. -32

问题16

函数 $f(x)$ 在 $x=b$ 处导数存在，为 $f’(b)$。则 $\lim_{h \to 0} \frac{f(b + 4h) - f(b - 2h)}{2h}$

A. $f’(b)$

B. $\frac{1}{3} f’(b)$

C. $3 f’(b)$

D. $2 f’(b)$

问题17

对于矩阵 $A$，已知 Rank(A) = 3，以下哪项是K可能的值？
$$
A = \begin{bmatrix}
K & 1 & 1 & 1 \
1 & K & 1 & 1 \
1 & 1 & K & 1 \
1 & 1 & 1 & K
\end{bmatrix}
$$
A. K=-1

B. K=-3 或 K=-1

C. K=-3

D. k=3 或 K=-1

问题18

下面哪种情况是用图的深度优先遍历方法得到的结果

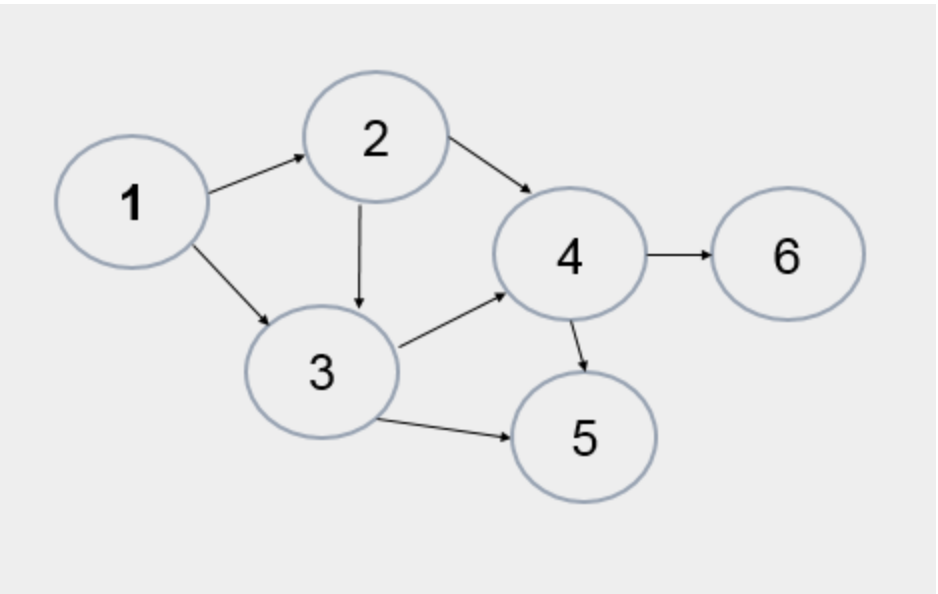
A. 1, 2, 3, 4, 5, 6

B. 1, 2, 4, 6, 5, 3

C. 1, 3, 5, 2, 4, 6

D. 1, 3, 2, 5, 4, 6

问题19

$Ax = 0$ 中 $A$ 是以下参数，哪个方程组有非零解？

A
$$
\begin{bmatrix}
-3 & 4 & -8 \
-2 & 5 & 5
\end{bmatrix}
$$
B
$$
\begin{bmatrix}
2 & -5 & 8 \
-2 & -7 & 1\
4 & 2 & 7
\end{bmatrix}
$$
C
$$
\begin{bmatrix}
-3 & 4 & -8 \
-2 & 5 & 4
\end{bmatrix}
$$
D
$$
\begin{bmatrix}
2 & -5 & 9 \
-2 & -7 & 1 \
4 & 2 & 7
\end{bmatrix}
$$

问题20

给一个整数数组，需要快速查找指定的一个整数是否在其中，需要哪些操作

A. 二分查找

B. 排序

C. 排序，二分查找

D. 顺序遍历

问题21

若 $f(x) = \int_{x}^{x^3} e^{-t^2} dt$，则 $f’(x) =$

A. $3x^2e^{-x^6} - e^{-x^2}$

B. $2x e^{-x^6} - e^{-x}$

C. $2x e^{-x^4} - e^{-x^2}$

D. $3x^2 e^{-x^6} - e^{-x}$

问题22

给定一组数据，以下哪种方法可以检验数据是否服从正态分布？

A. Q-Q图

B. Wilcoxon符号秩检验

C. K-S检验

D. t检验

问题23

关于秩统计量，下列说法正确的是：

A. 需要总体分布符合特定分布

B. 需要总体参数满足一定条件

C. 不需要总体分布符合特定分布

D. 检验统计量与总体分布的具体参数无关

问题24

下列关于协方差和相关系数的说法，正确的是？(假定X、Y是两个变量)

A. 协方差的正或负，反映两个变量X、Y是同向变化或反向变化

B. 协方差的绝对值，反映两个变量X、Y同向或反向变化的程度

C. 两个变量的相关系数是消除量纲和标准化之后的特殊的协方差

D. 相关系数反应两个变量每单位变化的相似程度

问题25

克莱姆法则是线性代数中一个关于求解线性方程组的定理。对于一个具有N个方程、N个未知数的线性方程组，下列说法正确的是：

A. 当方程组的系数行列式不等于零时，则方程组一定有解

B. 如果方程组有两个不同的解，那么方程组的系数行列式必定等于零

C. 如果方程组的系数行列式等于零，那么方程组一定无解

D. 当方程组的系数行列式不等于零时，则方程组可能有多组解

问答题

问题1

试论述机器学习模型中的偏差 (Bias) 和方差 (Variance)，并说明各种情况下的解决办法。

问题2

请简诉数理统计中假设检验的基本步骤。

问题3

假如你现在能够拿到微信用户的定位信息 (位置信息)，比如用户每一分钟会上传自己的位置到后台。请发挥你的想象力，这些定位数据能够做哪些事情，可以创造哪些社会价值。

Posted on Edited on

问题描述

Write a function that takes an unsigned integer and returns the number of ‘1’ bits it has (also known as the Hamming weight).

For example, the 32-bit integer ‘11’ has binary representation 00000000000000000000000000001011, so the function should return 3.

Related Topics: Bit Manipulation

原问题：191. Number of 1 Bits

解决方案

这个问题需要要用到位运算中的与运算&，与运算规则如下所示

1
2
3
4
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1

方案1

第一个解决方案是先判断数字二进制表示中最右边一位是不是1；接着把输入的数字右移一位，此时原来处于从右边数起的第二位被移到最右边了，再判断是不是1；这样每次移动一位，直到数字变成0为止。这个方案关键之处在于怎么判断一个数字的二进制表示的最右边一位是不是1。其实这个可以用与运算解决，只要把这个数字和1做与运算看结果是不是0就知道了，如果数字与1做与运算的结果是1，则表示数字的二进制表示的最右边一位是1，否则是0。

补充：这个解决方案针对无符号数字有效，对于有符号数字无效，因为有符号数字右移时，最高位会补1，此时如果使用数字变为0作为循环结束条件时，会陷入死循环，因此应该用for循环，循环次数为数字二进制的位数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution
{
public:
    int hammingWeight(uint32_t n)
    {
        int num_bits;

        num_bits = 0;
        while (n) {
            if (n & 1)
                num_bits++;
            n = n >> 1;
        }

        return num_bits;
    }
};

方案2

第二个解决方案是首先把数字与1做与运算，判断数字的二进制表示的最低位是不是1，接着把1左移1位，再和数字做与运算，就能判断数字的二进制表示的次低位是不是1，这样反复左移，直到所有位都被进行过与运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution
{
public:
    int hammingWeight(uint32_t n)
    {
        int num_bits;
        uint32_t flag;

        num_bits = 0;
        flag = 1;
        while (flag) {
            if (flag & n)
                num_bits++;
            flag = flag << 1;
        }

        return num_bits;
    }
};

这个方案的循环次数等于数字的二进制的位数，方案一的循环次数由该数字的二进制表示中的最高位1的位置决定，在最坏情况下，方案一的循环次数等于数字的二进制的位数。

Posted on Edited on

本文主要记录一些CMake的常见用法，例子代码都可以在CMakeDemos这里找到。

单个源文件

代码：Demo1

目录里面只有一个源文件，这个最简单的情况。目录结构如下所示

1
2
3
4
Demo1
├── CMakeLists.txt
├── build
└── main.cpp

文件 CMakeLists.txt 内容如下

1
2
3
4
5
6
7
8
# CMake 最低版本号要求
cmake_minimum_required(VERSION 3.9)

# 项目信息
project(Demo1)

# 指定生成目标
add_executable(Demo main.cpp)

符号#后面的内容被认为是注释。由add_executable知道，最终编译出的可执行文件是 Demo。

编译项目

如果在源码目录中直接使用命令cmake .生成Makefile文件的话，会发现目录多出很多文件，这样会导致目录内容很乱，通常做法是在一个目录里面生成CMake的临时文件，这里选择在目录 build 中生成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
➜  Demo1 git:(master) cd build
➜  build git:(master) cmake ..
-- The C compiler identification is AppleClang 8.0.0.8000042
-- The CXX compiler identification is AppleClang 8.0.0.8000042
-- Check for working C compiler: /Library/Developer/CommandLineTools/usr/bin/cc
-- Check for working C compiler: /Library/Developer/CommandLineTools/usr/bin/cc -- works
-- Detecting C compiler ABI info
-- Detecting C compiler ABI info - done
-- Detecting C compile features
-- Detecting C compile features - done
-- Check for working CXX compiler: /Library/Developer/CommandLineTools/usr/bin/c++
-- Check for working CXX compiler: /Library/Developer/CommandLineTools/usr/bin/c++ -- works
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-- Configuring done
-- Generating done
-- Build files have been written to: /Users/luowanqian/Documents/Project/CMakeDemos/Demo1/build
➜  build git:(master) make
Scanning dependencies of target Demo
[ 50%] Building CXX object CMakeFiles/Demo.dir/main.cpp.o
[100%] Linking CXX executable Demo
[100%] Built target Demo
➜  build git:(master) ./Demo
Sqrt(2) is 1.41421
➜  build git:(master)

进入build目录，然后使用命令cmake ..生成Makefile文件，然后使用make命令编译得到可执行文件Demo。

同一个目录，多个源文件

代码：Demo2

在同一个目录里面，有个多个源文件，此时目录结构如下所示

1
2
3
4
5
6
Demo2
├── CMakeLists.txt
├── MathFunctions.cpp
├── MathFunctions.h
├── build
└── main.cpp

此时 MathFunctions.cpp 里面实现了一个函数 mysqrt，main.cpp 会调用这个函数。此时文件 CMakeLists.txt 的内容如下

1
2
3
4
5
6
7
8
# CMake 最低版本号要求
cmake_minimum_required(VERSION 3.9)

# 项目信息
project(Demo2)

# 指定生成目标
add_executable(Demo main.cpp MathFunctions.cpp)

大致内容同前一节的所写的那样，只不过add_executable里面多了 MathFunctions.cpp 项。

多个目录，多个源文件

代码：Demo3

有时候我们不想把所有源文件放到同一个目录里面，想根据实现的功能放到不同的目录中，前面的 MathFunctions.cpp 实现了数学函数功能，因此这里把它放入 Math 目录中，此时目录结构如下

1
2
3
4
5
6
7
8
Demo3
├── CMakeLists.txt
├── build
├── main.cpp
└── math
    ├── CMakeLists.txt
    ├── MathFunctions.cpp
    └── MathFunctions.h

对于这种情况，需要分别在项目根目录 Demo3 和 math 目录中分别编写 CMakeLists.txt 文件。在项目编译时，现将 math 目录里的文件编译成静态库再链接到程序 Demo 中。

根目录CMakeLists.txt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# CMake 最低版本号要求
cmake_minimum_required(VERSION 3.9)

# 项目信息
project(Demo3)

# 添加 math 子目录
add_subdirectory(math)

# 添加 math 到头文件搜索路径
include_directories(math)

# 指定生成目标
add_executable(Demo main.cpp)

# 添加链接库
target_link_libraries(Demo MathFunctions)

文件的使用命令add_subdirectory添加子目录 math，这个命令很类似Makefile中的include命令，使用该命令后，CMake会处理 math 目录下的 CMakeLists.txt。这里还用了命令include_directories，主要是文件 main.cpp 会调用头文件 MathFunctions.h。链接静态库使用命令target_link_libraries，其中 MathFunctions 是静态库的名称，定义在 math 目录的 CMakeLists.txt 中。

math目录CMakeLists.txt

1
add_library(MathFunctions MathFunctions.cpp)

子目录的 CMakeLists.txt 文件内容如上，使用命令add_library命令将本目录的源文件编译为静态链接库，名称为 MathFunctions。

自定义编译选项

代码：Demo4

CMake可以项目设置编译选项，例如可以将 MathFunctions 库设为一个可选的库，如果该选项为 ON，则使用该库中的函数来进行运算，否则使用标准库的数学函数进行运算。首先看看项目目录的结构

1
2
3
4
5
6
7
8
9
Demo4
├── CMakeLists.txt
├── build
├── config.h.in
├── main.cpp
└── math
    ├── CMakeLists.txt
    ├── MathFunctions.cpp
    └── MathFunctions.h

目录中比上一节的目录结构中多了一个文件 config.h.in，CMake会将文件 config.h.in 转换成 config.h，这个头文件主要是定义了一些宏，源文件可以包含这个头文件，根据里面调用的宏来确定是否调用某个功能，所谓编译选项说白就是一堆宏。上面描述可能有点抽象，下面详细介绍各个文件内容

根目录CMakeLists.txt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# CMake 最低版本号要求
cmake_minimum_required(VERSION 3.9)

# 项目信息
project(Demo3)

# 是否使用 MathFunctions 库选项
option(USE_MYMATH "Use provided math implementation" ON)

# 生成一个配置头文件
configure_file(
    "${PROJECT_SOURCE_DIR}/config.h.in"
    "${PROJECT_BINARY_DIR}/config.h"
)

# 是否加入 MathFunctions 库
if (USE_MYMATH)
    include_directories("${PROJECT_SOURCE_DIR}/math")
    add_subdirectory(math)
    set(EXTRA_LIBS ${EXTRA_LIBS} MathFunctions)
endif(USE_MYMATH)

# 使得 CMake 可以找到生成的 config.h
include_directories("${PROJECT_BINARY_DIR}")

# 指定生成目标
add_executable(Demo main.cpp)

# 添加链接库
target_link_libraries(Demo ${EXTRA_LIBS})

文件中configure_file命令用于生成配置头文件 config.h，这个头文件由CMake从 config.h.in 中生成，config.h.in 这个文件里面有用户自己定义的编译选项，其中 USE_MYMATH 就是定义在文件 config.h.in 中，这里使用命令 option 默认开启这个选项，然后后面的 if 语句根据 USE_MYMATH 变量的值来决定是否使用我们自己的编写的数学函数库，由于 USE_MYATH 为 ON，所以默认是使用我们自己的库。

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include <cmath>

#include "config.h"

#ifdef USE_MYMATH
#include "MathFunctions.h"
#endif
using namespace std;

int main()
{
#ifdef USE_MYMATH
    cout << "Now we use our own Math library." << endl;
    cout << "Sqrt(2) is " << mysqrt(2) << endl;
#else
    cout << "Now we use the standard libary." << endl;
    cout << "Sqrt(2) is " << sqrt(2) << endl;
#endif

    return 0;
}

源文件中可以使用我们定义 USE_MYMATH 来决定是否调用自己编写的库，要使用这个宏，需要包含 config.h 这个头文件，这个头文件是CMake根据 config.h.in 生成。

config.h.in

1
#cmakedefine USE_MYMATH

编译选项 USE_MYMATH 定义在这个文件中。

编译项目

现在编译这个项目，为了便于交互式的修改编译选项，可以使用 ccmake 命令：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
➜  Demo4 git:(master) ✗ ll
total 24
-rw-r--r--  1 luowanqian  staff   722B  4  3 10:07 CMakeLists.txt
drwxr-xr-x  2 luowanqian  staff    68B  4  3 10:11 build
-rw-r--r--  1 luowanqian  staff    23B  4  2 08:46 config.h.in
-rw-r--r--  1 luowanqian  staff   398B  4  2 08:54 main.cpp
drwxr-xr-x  5 luowanqian  staff   170B  4  2 08:44 math
➜  Demo4 git:(master) ✗ cd build
➜  build git:(master) ✗ cmake ..
-- The C compiler identification is AppleClang 8.0.0.8000042
-- The CXX compiler identification is AppleClang 8.0.0.8000042
-- Check for working C compiler: /Library/Developer/CommandLineTools/usr/bin/cc
-- Check for working C compiler: /Library/Developer/CommandLineTools/usr/bin/cc -- works
-- Detecting C compiler ABI info
-- Detecting C compiler ABI info - done
-- Detecting C compile features
-- Detecting C compile features - done
-- Check for working CXX compiler: /Library/Developer/CommandLineTools/usr/bin/c++
-- Check for working CXX compiler: /Library/Developer/CommandLineTools/usr/bin/c++ -- works
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-- Configuring done
-- Generating done
-- Build files have been written to: /Users/luowanqian/Documents/Project/CMakeDemos/Demo4/build
➜  build git:(master) ✗ ccmake ..

从中可以找到刚刚定义的USE_MYMATH选项，按键盘的方向键可以在不同的选项窗口间跳转，按下enter键可以修改该选项。修改完成后可以按下c键完成配置，之后再按g键确认生成 Makefile。下面分别展示将USE_MYMATH设为ON和OFF得到的结果：

USE_MYMATH 设为 ON

1
2
3
4
5
6
7
8
9
10
11
12
13
➜  build git:(master) ✗ make
Scanning dependencies of target MathFunctions
[ 25%] Building CXX object math/CMakeFiles/MathFunctions.dir/MathFunctions.cpp.o
[ 50%] Linking CXX static library libMathFunctions.a
[ 50%] Built target MathFunctions
Scanning dependencies of target Demo
[ 75%] Building CXX object CMakeFiles/Demo.dir/main.cpp.o
[100%] Linking CXX executable Demo
[100%] Built target Demo
➜  build git:(master) ✗ ./Demo
Now we use our own Math library.
Sqrt(2) is 1.41421
➜  build git:(master) ✗

USE_MYMATH 设为 OFF

1
2
3
4
5
6
7
8
➜  build git:(master) ✗ make
Scanning dependencies of target Demo
[ 50%] Building CXX object CMakeFiles/Demo.dir/main.cpp.o
[100%] Linking CXX executable Demo
[100%] Built target Demo
➜  build git:(master) ✗ ./Demo
Now we use the standard libary.
Sqrt(2) is 1.41421

参考

  1. CMake入门实战
  2. CMake Tutorial

Posted on Edited on

问题描述

Given an array of integers that is already sorted in ascending order, find two numbers such that they add up to a specific target number.

The function twoSum should return indices of the two numbers such that they add up to the target, where index1 must be less than index2. Please note that your returned answers (both index1 and index2) are not zero-based.

You may assume that each input would have exactly one solution and you may not use the same element twice.

Input: numbers={2, 7, 11, 15}, target=9

Output: index1=1, index2=2

Related Topics: Array, Two Pointers, Binary Search

原问题：167. Two Sum II - Input array is sorted

解决方案

考虑我们在数组中选择两个数字，如果它们的和等于输入的 target，那么我们就找到了要找的这两个数字。如果和小于 target 呢？我们希望两个数字的和再大一点。由于数组已经排序好了，我们可以考虑选择较小的数字后面的数字。因为排在后面的数字要大一些，那么两个数字的和也要大一些，就有可能等于输入的数字 target 了。同样，当两个数字的和大于输入 target 的时候，我们可以选择较大数字前面的数字，因为排在数字前面的数字要小一些。

根据上面的思路，我们可以设定两个指针 point1 和 point2，point1 指向数组的第一个元素，point2 指向数组的最后一个元素，然后根据上面的判断准则，当两个指针指向的数字之和小于 target 时，指针 point1 加一，反之指针 point2 减一，通过不断地迭代，直到数组被遍历完。实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <vector>
using namespace std;

class Solution
{
public:
    vector<int> twoSum(vector<int>& numbers, int target)
    {
        vector<int> idx;

        if (numbers.size() < 2)
            return idx;

        int left, right;
        left = 0;
        right = numbers.size()-1;
        while (left < right) {
            if (numbers[left] + numbers[right] < target) {
                left++;
            } else if (numbers[left] + numbers[right] > target) {
                right--;
            } else {
                idx.push_back(left+1);
                idx.push_back(right+1);
                break;
            }
        }

        return idx;
    }
};

int main()
{
    Solution solu;
    vector<int> nums {2, 7, 11, 15};
    int target = 9;
    vector<int> idx = solu.twoSum(nums, target);
    if (idx.size() < 2)
        cout << "Not found" << endl;
    else
        cout << "index1=" << idx[0]
             << ", index2=" << idx[1] << endl;

    return 0;
}

Posted on Edited on

问题描述

Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Note: The solution set must not contain duplicate triplets.

For example, given array S = [-1, 0, 1, 2, -1, -4],

A solution set is:

[ [-1, 0, 1], [-1, -1, 2] ]

Related Topics: Array, Two Pointers

原问题：15. 3Sum

解决方案

这个问题是 2Sum 问题的一个扩展，题目不仅要求输出满足条件的数字对，而且要保证数字对不能重复。咋一看问题有点无从下手，但是 3Sum 问题可以转换成 2Sum 问题，如果我们固定数字 $a$，那么剩下的问题就变成 2Sum 问题了，也就是寻找数字 $b$ 和数字 $c$，使得 $b+c = -a$，这里有个问题就是如何选取数字 $a$，看题目给的例子的输出，我们发现输出的数字对里面的元素是有序的，这里启示我们可以作一个假设，那就是 $a \le b \le c$，因此关于如何选取数字 $a$ 可以先对输入的数组进行从小到大排序，然后从头开始遍历数组，这里设访问到的第 $i$ 个元素作为数字 $a$，然后数组 $i+1$ 的元素到最后一个元素作为数字 $b$ 和数字 $c$ 的搜索区间，此时问题已经变成一个有序数组的 2Sum 问题，这个问题解决思想类似LeetCode的一道题目—Two Sum II - Input array is sorted，需要两个指针移动来进行搜索 (关于这个问题，可以参考我的文章)，区别在于这里需要找到多组数字 $b$ 和数字 $c$。

这道题目还有一个难点，就是解决重复的数字对，根据前面的描述，我们所遇到的重复有两个，一个是数字 $a$ 会重复，一个是数字对 $(b, c)$ 会重复，解决方案如下：

  • 遇到数字 $a$ 重复，跳到下一个数字作为数字 $a$
  • 在搜索满足条件的数字对 $(b, c)$ 时，如果搜索到满足条件的数字对 $(b, c)$ 后，两个指针同时移动，直到指针指向的元素不是之前搜索到的数字对 $(b, c)$

说了这么多，读者理解起来可能有点困难，还是看实现代码更容易理解前面所说的思路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

class Solution
{
public:
    vector<vector<int>> threeSum(vector<int>& nums)
    {
        vector<vector<int>> triplets;

        if (nums.size() < 3)
            return triplets;

        sort(nums.begin(), nums.end());
        int left, right, target;
        for (int i=0; i<nums.size(); i++) {
            if (i == 0 || nums[i] > nums[i-1]) {
                target = -nums[i];
                left = i+1;
                right = nums.size()-1;
                while (left < right) {
                    if (nums[left] + nums[right] < target) {
                        left++;
                    } else if (nums[left] + nums[right] > target) {
                        right--;
                    } else {
                        triplets.push_back(vector<int>{nums[i], nums[left], nums[right]});
                        left++;
                        right--;
                        while (left < right && nums[left] == nums[left-1])
                            left++;
                        while (left < right && nums[right] == nums[right+1])
                            right--;
                    }
                }
            }
        }

        return triplets;
    }
};

int main()
{
    Solution solu;
    //vector<int> nums {1,0,1,2,-1,-4};
    vector<int> nums {0,-5,3,-4,1,3,-4,-2,-2,-2,0,3,0,1,-4,-2,0};

    vector<vector<int>> triplets = solu.threeSum(nums);
    for (int i=0; i<triplets.size(); i++) {
        for (int j=0; j<triplets[i].size(); j++) {
            cout << triplets[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

Posted on Edited on

模型介绍

Softmax回归 (或者称多项Logistic回归) 是Logistic回归的一般化形式，这是多分类模型，二项Logistic回归是其特殊情况，因为类别只有两类。类似二项Logistic回归模型 (关于二项Logistic回归模型，可以参考我的文章) ，Softmax回归模型也是由条件概率 $P(Y | X)$ 表示，$Y$ 的取值不再是 ${0, 1}$ 两类，而是 ${1, 2, \ldots, K}$，其中 $K$ 是类别数，这里类别不从 $0$ 开始是为了后面公式推导方便，实际编码中，类别映射通常都从 $0$ 开始。我们定义不同类别对应的条件概率为：
$$
\begin{align}
P(Y = 1 | x) & = \frac{e^{\theta^T_1 x + b}}{\sum_{j=1}^K e^{\theta_j^T x + b}} \
P(Y = 2 | x) & = \frac{e^{\theta^T_2 x + b}}{\sum_{j=1}^K e^{\theta_j^T x + b}} \
\vdots \
P(Y = K | x) & = \frac{e^{\theta^T_K x + b}}{\sum_{j=1}^K e^{\theta_j^T x + b}}
\end{align}
$$
这里 $x \in R^{d}$ 是输入，$Y \in {1, 2, \ldots, K}$ 输出，$\theta_k\in R^{d} ; (k=1,\ldots, K)$ 和 $b \in R$ 是未知参数。 同二项Logistic模型那样，对于给定的输入 $x$，分别计算 $x$ 属于不同类别的概率，然后 $x$ 的类别分到概率值最大的那一类。有时为了方便，将权值向量 $\theta_k$ 和输入向量 $x$ 加以扩充，仍记作 $\theta_k$ 和 $x$，即 $\theta_k = [\theta_{k1}, \ldots, \theta_{kd}, b]^T \in R^{d+1}$，$x = [x_1, x_2, \ldots, x_d, 1] \in R^{d+1}$，此时条件概率为：
$$
P(Y = k | x) = \frac{e^{\theta^T_k x}}{\sum_{j=1}^K e^{\theta_j^T x}} \quad (k=1, 2, \ldots, K)
$$

参数估计

模型参数估计方法同二项Logistic回归模型那样，使用极大似然估计法 (MLE) 进行估计。已知输入的训练数据集 $T = { (x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N) }$，其中 $x_i = [x_{i1}, \ldots, x_{id}, 1]^T \in R^{d+1}$，$y_i \in {1, 2, \ldots, K}$，待求的参数为 $\theta_k = [\theta_{k1}, \ldots, \theta_{kd}, b] \in R^{d+1} ; (k=1, 2, \ldots, K)$。前面不同类别的条件概率写成一条式子如下：
$$
P( Y = y | x) = \prod_{k=1}^K \left(\frac{e^{\theta^T_k x}}{\sum_{j=1}^K e^{\theta_j^T x}}\right)^{1{ y = k}}
$$
这里 $1{ \cdot }$ 为指indicator函数，定义为
$$
1{x } = \begin{cases}
1 & \text{x is a true statement} \
0 & \text{x is a false statement}
\end{cases}
$$
定义似然函数为：
$$
L(\theta_1, \ldots, \theta_K) = \prod_{i=1}^N \prod_{k=1}^K \left(\frac{e^{\theta^T_k x_i}}{\sum_{j=1}^K e^{\theta_j^T x_i}}\right)^{1{ y_i = k}}
$$
对数似然函数为：
$$
\ln(L(\theta_1, \ldots, \theta_K)) = \sum_{i=1}^N \sum_{k=1}^K 1{ y_i = k } \ln\left( \frac{e^{\theta^T_k x_i}}{\sum_{j=1}^K e^{\theta_j^T x_i}} \right)
$$
对 $\ln(L(\theta_1, \ldots, \theta_K))$ 求最大值，得到 $\theta_k$ 的估计值，在实现时，通常转换为求最小值，即对 $\ln(L(\theta_1, \ldots, \theta_K))$ 求最大值转换成对 $-\ln(L(\theta_1, \ldots, \theta_K))$ 求最小值：
$$
\min_{\theta_1, \ldots, \theta_K} -\sum_{i=1}^N \sum_{k=1}^K 1{ y_i = k } \ln \left( \frac{e^{\theta^T_k x_i}}{\sum_{j=1}^K e^{\theta_j^T x_i}} \right)
$$

模型实现

根据前面描述，模型参数估计主要是要求解下面这个优化问题：
$$
\min_{\theta_1, \ldots, \theta_K} -\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1{ y_i = k } \ln \left( \frac{e^{\theta^T_k x_i}}{\sum_{j=1}^K e^{\theta_j^T x_i}} \right)
$$
这里多乘一个系数 $\frac{1}{N}$ 并不会改变最优解的大小。上述问题可以用梯度下降法或者拟牛顿法进行求解，在求解过程中，需要计算目标函数的梯度，接下来推导梯度矩阵的表达式，这里首先令函数 $J(\theta_1, \ldots, \theta_K)$ 为损失函数 (目标函数)：
$$
J(\theta_1, \ldots, \theta_K) = -\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1{ y_i = k } \ln \left( \frac{e^{\theta^T_k x_i}}{\sum_{j=1}^K e^{\theta_j^T x_i}} \right)
$$

梯度推导

为了表示方便，这里定义参数矩阵 $\theta$ 为
$$
\theta = \begin{bmatrix}
\theta_1 & \theta_2 & \cdots & \theta_K
\end{bmatrix} = \begin{bmatrix}
\theta_{11} & \theta_{21} & \cdots & \theta_{K1} \
\theta_{12} & \theta_{22} & \cdots & \theta_{K2} \
\vdots & \vdots & & \vdots \
\theta_{1d} & \theta_{2d} & \cdots & \theta_{Kd} \
\end{bmatrix}
$$
矩阵 $\theta$ 的大小为 $R^{d \times K}$，每一列为参数向量 $\theta_k , (k=1, \ldots, K)$，因此损失函数 $J(\theta_1, \ldots, \theta_K)$ 简写为 $J(\theta)$。为了后面推导方便，首先将损失函数分解为两部分：
$$
\begin{align}
J(\theta) & = -\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1{ y_i = k } \ln \left( \frac{e^{\theta^T_k x_i}}{\sum_{j=1}^K e^{\theta_j^T x_i}} \right) \
& = -\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \ln ( e^{\theta^T_k x_i} ) +\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \ln (\sum_{j=1}^K e^{\theta_j^T x_i}) \
& = -\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } (\theta^T_k x_i )+\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \ln (\sum_{j=1}^K e^{\theta_j^T x_i}) \
\end{align}
$$
令这两部分分别为 $f(\theta)$ 和 $g(\theta)$
$$
\begin{align}
f(\theta) &= -\frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } (\theta^T_k x_i ) \
g(\theta) & = \frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \ln (\sum_{j=1}^K e^{\theta_j^T x_i})
\end{align}
$$
损失函数 $J(\theta)$ 对矩阵 $\theta$ 某一个元素 $\theta_{pq}$ ($\theta_{pq}$ 代表参数向量 $\theta_q$ 的第 $p$ 个元素) 的偏导为：
$$
\frac{\partial{J(\theta)}}{\partial{\theta_{pq}}} = \frac{\partial{f(\theta)}}{\partial{\theta_{pq}}} + \frac{\partial{g(\theta)}}{\partial{\theta_{pq}}}
$$

第一部分

函数 $f(\theta)$ 对 $\theta_{pq}$ 偏导可以得到：
$$
\begin{align}
\frac{\partial{f(\theta)}}{\partial{\theta_{pq}}} & = -\frac{1}{N} \sum_{i=1}^N 1{ y_i = q } \frac{\partial{\theta_q^T x_i}}{\partial{\theta_{pq}}} \
& = -\frac{1}{N} \sum_{i=1}^N 1{ y_i = q } x_{ip}
\end{align}
$$

第二部分

函数 $g(\theta)$ 对 $\theta_{pq}$ 可以得到：
$$
\begin{align}
\frac{\partial{g(\theta)} }{\partial{\theta_{pq}}} & = \frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \frac{ \partial\ln(\sum_{j=1}^K e^{\theta_j^Tx_i}) }{ \partial{\theta_{pq}} } \
& = \frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \frac{1}{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \frac{\partial{e^{\theta_q^T x_i}} }{\partial{\theta_{pq}}} \
& = \frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \frac{ e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \frac{ \partial{\theta^T_q x_i} }{\partial{\theta_{pq}}} \
& = \frac{1}{N} \sum_{i=1}^N \sum_{k=1}^K 1 { y_i = k } \frac{ x_{ip} e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \
& = \frac{1}{N} \sum_{i=1}^N \frac{ x_{ip} e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \sum_{k=1}^K 1 { y_i = k }
\end{align}
$$
由于 $\sum_{k=1}^K 1 { y_i = k } = 1$，则最终可以得到
$$
\frac{\partial{g(\theta)} }{\partial{\theta_{pq}}} = \frac{1}{N} \sum_{i=1}^N \frac{ x_{ip} e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} }
$$

综合

综合第一部分和第二部分的推导，可以得到
$$
\begin{align}
\frac{\partial{J(\theta)}}{\partial{\theta_{pq}}} & = -\frac{1}{N} \sum_{i=1}^N 1{ y_i = q } x_{ip} + \frac{1}{N} \sum_{i=1}^N \frac{ x_{ip} e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \
& = -\frac{1}{N} \sum_{i=1}^N \left[ 1{ y_i = q } x_{ip} - \frac{ x_{ip} e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \right] \
& = -\frac{1}{N} \sum_{i=1}^N \left[ x_{ip} \left( 1{ y_i = q } - \frac{ e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \right) \right]
\end{align}
$$
如果要表示梯度向量 $\frac{\partial{J(\theta)}}{\partial{\theta_q}}$，可以写成如下形式：
$$
\frac{\partial{J(\theta)}}{\partial{\theta_q}} = -\frac{1}{N} \sum_{i=1}^N \left[ x_{i} \left( 1{ y_i = q } - \frac{ e^{\theta_q^T x_i} }{ \sum_{j=1}^K e^{\theta_j^Tx_i} } \right) \right]
$$

参考

  1. UFLDL Softmax Regression

Posted on Edited on

二项Logistic回归模型

二项Logistic回归模型是一种分类模型，由条件概率分布 $P(Y|X)$ 表示，这里的随机变量取值为实数，随机变量 $Y$ 取值为 0 或 1，这个条件概率分布是未知的，需要通过监督学习方法来进行估计。条件概率分布如下表示：
$$
\begin{align}
P(Y=1 | x) & = \frac{e^{x^T \beta + b}}{1 + e^{x^T\beta + b}} = \frac{1}{1 + e^{-x^T \beta + b}} \
P(Y = 0 | x) & = \frac{1}{1 + e^{x^T \beta + b}}
\end{align}
$$
这里，$x\in R^d$ 是输入，$Y \in {0, 1}$ 是输出，$\beta \in R^d$ 和 $b$ 是参数。模型参数是未知的，需要进行模型训练获得，当获得模型参数时，对于一个新的输入实例 $x$，根据上面式子分别求出条件概率 $P(Y=1 | x)$ 和 $P(Y=0|x)$，比较两个条件概率值的大小，将实例 $x$ 分到较大的那一类。

模型参数估计

模型参数估计通常使用极大似然估计法 (MLE) 进行估计。已知输入的训练数据集 $T = {(x_1, y_1), \ldots, (x_N, y_N)}$，其中 $x_i = [x_{i1}, x_{i2}, \ldots, x_{id}]^T \in R^d$，$y_i \in {0, 1}$，待求的参数为 $\beta = [\beta_1, \beta_2, \ldots, \beta_d]^T \in R^d$ 和 $b \in R$。设：
$$
\begin{align}
P(Y=1|x) & = \phi(x) \
P(Y =0 | x) & = 1 - \phi(x)
\end{align}
$$
两个结合成一个式子可以写成如下表示：
$$
P(Y = y | x) = \phi(x)^{y} (1 - \phi(x))^{1- y}
$$
定义似然函数为：
$$
L(\beta, b) = \prod_{i=1}^N \phi(x_i)^{y_i} (1 - \phi(x_i))^{1-y_i}
$$

则对数似然函数为：
$$
\begin{align}
\ln (L(\beta, b)) & = \ln \left( \prod_{i=1}^N \phi(x_i)^{y_i} (1 - \phi(x_i))^{1-y_i} \right) \
& = \sum_{i=1}^N \left[ y_i \ln(\phi(x_i)) + (1- y_i) \ln(1-\phi(x_i))\right] \
& = \sum_{i=1}^N \left[ y_i \ln\left(\frac{\phi(x_i)}{1 - \phi(x_i)} \right) + \ln(1- \phi(x_i)) \right]
\end{align}
$$
根据前面模型描述，可以知道
$$
\phi(x) = \frac{e^{x^T \beta + b}}{1 + e^{x^T\beta + b}}
$$
则 $\frac{\phi(x)}{1-\phi(x)}$ 为
$$
\frac{\phi(x)}{1 - \phi(x)} = e^{x^T \beta + b}
$$
因此对数似然函数为：
$$
\begin{align}
\ln(L(\beta, b)) & = \sum_{i=1}^N \left[ y_i \ln(e^{x_i^T \beta}) + \ln\left( \frac{1}{1 + e^{x_i^T\beta + b}} \right) \right] \
& = \sum_{i=1}^N \left[ y_i (x_i^T \beta) - \ln(1 + e^{x_i^T\beta + b}) \right]
\end{align}
$$
对 $\ln(L(\beta, b))$ 求最大值，得到 $\beta$ 和 $b$ 的估计值，不过在实现时，通常转化为求解最小值，即对 $\ln(L(\beta, b))$ 求最大值转换成对 $-\ln(L(\beta, b))$ 求最小值：
$$
\min_{\beta, b} \sum_{i=1}^N \left[ \ln(1 + e^{x_i^T\beta + b}) - y_i (x_i^T \beta) \right]
$$

模型实现

根据前面描述，模型参数估计主要是要求解

$$
\min_{\beta, b} \frac{1}{N} \sum_{i=1}^N \left[ \ln(1 + e^{x_i^T\beta + b}) - y_i (x_i^T \beta) \right]
$$

这里多乘一个系数 $\frac{1}{N}$ 并不会改变最优解的大小。上述问题可以采用梯度下降法或者拟牛顿法进行求解，在求解过程中，需要计算目标函数的梯度。令函数 $f(\beta, b)$ 为：
$$
f(\beta, b) = \sum_{i=1}^N \left[ \ln(1 + e^{x_i^T\beta + b}) - y_i (x_i^T \beta) \right]
$$
则函数 $f(\beta, b)$ 对 $\beta_k ; (k=1, \ldots, d)$ 的偏导为
$$
\begin{align}
\frac{\partial{f(\beta, b)}}{\partial \beta_k} & = \frac{1}{N} \sum_{i=1}^N \left( \frac{x_{ik}e^{\beta^T x_i + b}}{1 + e^{\beta^T x_i + b}} -x_{ik} y_i \right) \
& = \frac{1}{N} \sum_{i=1}^N \left( \frac{x_{ik}}{1 + e^{-(\beta^T x_i + b)}} - x_{ik}y_i \right)
\end{align}
$$
令矩阵 $X \in R^{N \times d}$ 为
$$
X = \begin{bmatrix}
x_{11} & \ldots & x_{1d} \
x_{21} & \ldots & x_{2d} \
\vdots & & \vdots \
x_{N1} & \ldots & x_Nd
\end{bmatrix} = \begin{bmatrix}
x_1^T \
x_2^T \
\vdots \
x_N^T
\end{bmatrix}
$$
则 $X\beta + b$ 为
$$
X \beta + b = [\beta^T x_1 + b , \ldots, \beta^T x_N + b]^T
$$
令函数 $g(x)$ 为 Sigmoid 函数，也就是
$$
g(x) = \frac{1}{1 + e^{-x}}
$$
则 $g(X \beta + b)$ 为
$$
g(X \beta + b) = \begin{bmatrix}
\frac{1}{1 + e^{-(\beta^T x_1 +b)}} \
\frac{1}{1 + e^{-(\beta^T x_2 +b)}} \
\vdots \
\frac{1}{1 + e^{-(\beta^T x_N +b)}}
\end{bmatrix}
$$
令 $Xt =X^T$，矩阵 $Xt$ 第 $k$ 行为 $Xt[k, :]$，则可以得到
$$
\sum_{i=1}^N \frac{x_{ik}}{1 + e^{-(\beta^T x_i + b)}} = Xt[k, :] g(X\beta + b)
$$
以及
$$
\sum_{i=1}^N x_{ik} y_i = Xt[k, :] y
$$
因此
$$
\begin{align}
\frac{\partial{f(\beta, b)}}{\partial \beta_k} & = \frac{1}{N} \sum_{i=1}^N \left( \frac{x_{ik}e^{\beta^T x_i + b}}{1 + e^{\beta^T x_i + b}} -x_{ik} y_i \right) \
& = \frac{1}{N} \sum_{i=1}^N \left( \frac{x_{ik}}{1 + e^{-(\beta^T x_i + b)}} - x_{ik}y_i \right) \
& = \frac{1}{N} Xt[k, :] \left(g(X\beta + b) - y \right)
\end{align}
$$
则可得
$$
\begin{bmatrix}
\frac{\partial f(\beta, b)}{\partial \beta_1} \
\frac{\partial f(\beta, b)}{\partial \beta_2} \
\vdots \
\frac{\partial f(\beta, b)}{\partial \beta_d}
\end{bmatrix} = \frac{1}{N} \begin{bmatrix}
Xt[1, :] \left(g(X\beta + b) - y\right) \
Xt[2, :] \left(g(X\beta + b) - y\right) \
\vdots \
Xt[N, :] \left(g(X\beta + b) - y\right)
\end{bmatrix} = \frac{1}{N} X^T (g(X\beta+b)- y)
$$
前面是求函数 $f(\beta, b)$ 对 $\beta_k$ 的偏导，对于偏置项 $b$，函数 $f(\beta, b)$ 对 $b$ 的偏导为
$$
\begin{align}
\frac{\partial f(\beta, b)}{\partial b} & = \frac{1}{N} \sum_{i=1}^N \left( \frac{e^{\beta^T x_i + b}}{1 + e^{\beta^T x_i + b}} - y_i \right) \
& = \frac{1}{N} \sum_{i=1}^N \left( \frac{1}{1 + e^{-(\beta^T x_i + b)}} - y_i \right) \
& = \frac{1}{N} 1^T (g(X\beta + b) - y)
\end{align}
$$

这里的 $1$ 代表元素全是1的列向量。综上可以得到，函数 $f(\beta, b)$ 的梯度为：
$$
\nabla f(\beta, b) = \begin{bmatrix}
\frac{1}{N} 1^T (g(X\beta + b) - y) \
\frac{1}{N} X^T (g(X\beta+b)- y)
\end{bmatrix}
$$
这个梯度向量第一个元素代表 $\frac{\partial f(\beta, b)}{\partial b}$。知道梯度向量的表示，我们可以用梯度下降法或拟牛顿法 (例如BFGS等) 来求解优化问题，我这里采用BFGS算法来进行求解，核心代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
import numpy as np
from scipy.optimize import minimize


class LogisticRegression:
    def __init__(self, alpha=1.0, max_iter=1000, tol=1e-4):
        self.alpha = alpha
        self.max_iter = max_iter
        self.tol = tol

    def sigmoid(self, x):
        return 1 / (1.0 + np.exp(-x))

    def objective(self, beta, X, y):
        n, _ = X.shape
        tmp = np.dot(X, beta[1:]) + beta[0]
        object = np.sum(np.log(1+np.exp(tmp))) - np.dot(y, tmp)

        return object / (1.0 * n)

    def gradient(self, beta, X, y):
        n, _ = X.shape
        tmp = self.sigmoid(np.dot(X, beta[1:]) + beta[0]) - y
        grads = []
        grads.append(np.sum(tmp)/(1.0*n))
        grads.extend(np.dot(X.T, tmp)/(1.0*n))

        return np.array(grads)

    def callback(self, beta):
        self.history.append(self.objective(beta, self.X, self.y))

    def fit(self, X, y):
        n, p = X.shape
        self.X = X
        self.y = y
        self.history = []

        # initialize
        beta0 = np.random.randn(p+1)

        res = minimize(self.objective, beta0, args=(X, y), method='BFGS',
                       jac=self.gradient, callback=self.callback)

        self.coef = res.x[1:]
        self.intercept = res.x[0]

        return self

    def predict(self, X):
        activation = self.sigmoid(np.dot(X, self.coef) + self.intercept)
        y = np.zeros(X.shape[0], dtype=np.int)
        y[activation >= 0.5] = 1

        return y

    def score(self, X, y):
        y_predict = self.predict(X)

        return np.mean(y == y_predict) * 100

    @property
    def coef_(self):
        return self.coef

    @property
    def intercept_(self):
        return self.intercept

    @property
    def history_(self):
        return self.history

全部相关的代码在：GitHub