ROC曲线绘制

介绍

关于ROC曲线的详细介绍，可以参考周志华的西瓜书 (《机器学习》)，本文主要介绍如何使用Python绘制该曲线。ROC曲线的纵轴是“真正例率” (True Positive Rate，简称TPR)，横轴是“假正例率” (False Positive Rate，简称FPR)，两者定义为：
$$
\begin{align}
TPR & = \frac{TP}{TP + FN} \
FPR & = \frac{FP}{TN + FP}
\end{align}
$$
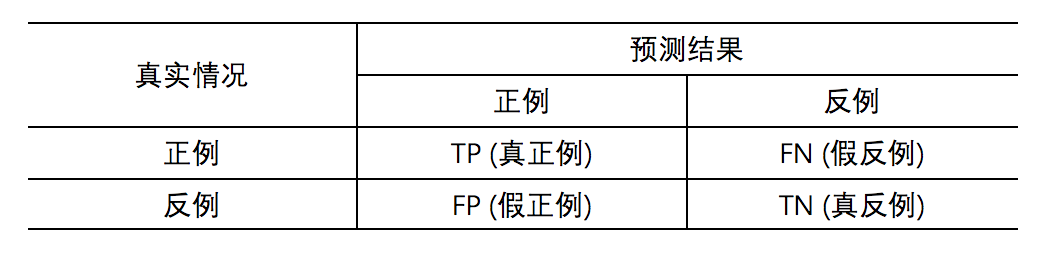
相关的符号定义为：

在现实任务中，我们获取有限个 (FPR, TPR) 坐标对来勾勒出ROC曲线。要获得多个坐标对需要多组二分类结果，而我们做二分类任务时，通常只能获取一组分类结果，此时我们利用这组结果生成多组分类结果，具体做法是：给定 $m$ 个正例和 $n$ 个反例，根据分类器的预测值对样例进行从大到小排序，然后把分类阈值设为样例预测值中最大的那个，将样例进行正反例分类，计算相应的TPR和FPR，然后令分类阈值依次设为每个样例的预测值，将样例进行正反例分类，接着计算TPR和FPR，重复这个操作，直到分类阈值取完所有样例的预测值。

关于分类器对样例的预测值，我们可以用分类器判定样例为正例的概率值，也可以用分类器对样例的评分值，预测值大于等于分类阈值时，分类器判定样例为正例，否则判定为负例。

例子

已知10样例的真实标签 (0: 反例，1: 正例) 以及分类器对该样例的评分值

1 2	y_true = [0, 1, 1, 0, 1, 0, 1, 1, 1, 0] y_score = [0.505, 0.6, 0.8, 0.52, 0.55, 0.53, 0.54, 0.9, 0.51, 0.7]

根据评分值将样例进行从大到小排序，可以得到

1 2	y_true = [1, 1, 0, 1, 1, 1, 0, 0, 1, 0] y_score = [0.9, 0.8, 0.7, 0.6, 0.55, 0.54, 0.53, 0.52, 0.51, 0.505]

将分类阈值设为 0.9，此时样例的分类为

1 2	y_true = [1, 1, 0, 1, 1, 1, 0, 0, 1, 0] y_predict = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]

可以得到 TP = 1，FP = 0，FN = 5，TN = 4，则可得到 TPR = 1/(1+5) = 1/6 以及 FPR = 0。接着将分类阈值设为 0.8，然后将样例进行正反例分类，接着计算相应的TPR和FPR，直到分类阈值取完所有评分值，最终可以得到下面的TPR和FPR列表

1 2	TPR = [0.16666667, 0.33333333, 0.33333333, 0.5, 0.66666667, 0.83333333, 0.83333333, 0.83333333, 1.0, 1.0] FPR = [0.0, 0.0, 0.25, 0.25, 0.25, 0.25, 0.5, 0.75, 0.75, 1.0]

然后根据这一系列的 (FPR, TPR) 坐标对画出ROC曲线。

实现

相关代码以及运用可以参考：GitHub

Scikit-learn实现

Scikit-learn库提供了一个名为 roc_curve 函数来获取FPR以及TRP，函数原型如下

1	sklearn.metrics.roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=True)

要想得到上面例子的计算结果，需要把 drop_intermediate 设为 False。

个人实现

我这里直接照搬[1]中的实现，贴出代码如下

def binary_clf_curve(y_true, y_score, pos_label=None):
    if pos_label is None:
        pos_label = 1.0

    # make y_true a boolean vector
    y_true = (y_true == pos_label)

    # sort scores
    desc_score_indices = np.argsort(y_score)[::-1]
    thresholds = y_score[desc_score_indices]

    fps = []
    tps = []
    for threshold in thresholds:
        # 大于等于阈值判定为 1 (正类)，否则为 0 (负类)
        y_predict = [1 if i >= threshold else 0 for i in y_score]
        # 预测值是否等于真实值
        result = [i == j for i, j in zip(y_true, y_predict)]
        # 预测值是否为 1 (正类)
        positive = [i == 1 for i in y_predict]

        # 预测为正类且预测错误
        fp = [(not i) and j for i, j in zip(result, positive)].count(True)
        # 预测为正类且预测正确
        tp = [i and j for i, j in zip(result, positive)].count(True)

        fps.append(fp)
        tps.append(tp)
    fps = np.array(fps)
    tps = np.array(tps)

    return fps, tps, thresholds


def roc_curve(y_true, y_score, pos_label=None):
    fps, tps, thresholds = binary_clf_curve(y_true, y_score, pos_label)

    fpr = fps / fps[-1]
    tpr = tps / tps[-1]

    return fpr, tpr, thresholds