K-means参数K的选择

介绍

对于K均值算法中聚类个数K的选择，通常有四种方法：

按需选择
观察法
手肘法
Gap Statistic方法

本文相关算法的代码以及实验在：GitHub

按需选择

简单地说就是按照建模的需求和目的来选择聚类的个数。比如说，一个游戏公司想把所有玩家做聚类分析，分成顶级、高级、中级、菜鸟四类，那么K=4；如果房地产公司想把当地的商品房分成高中低三档，那么K=3。按需选择法虽然合理，但是未必能保证在做K-Means时能够得到清晰的分界线。

观察法

观察法就是将数据可视化，然后用肉眼去观察这些数据点大概分成几堆。这个方法有个缺点，那就是数据维度不能太高，一般是二维或者三维，否则数据无法可视化出来。

手肘法

手肘法 (Elbow Method) 本质上也是一种间接的观察法。当我们对数据 ${ x_1, \ldots, x_N }$ 进行K均值聚类后，我们将得到 $K$ 个聚类的中心点 $\mu_k, k=1,2, \ldots, K$，以及数据点 $x_i$ 所对应的簇 $C_k, k=1, 2, \ldots, K$，每个簇中有 $n_k$ 个数据点。我们定义每个簇中的所有点相互之间的距离的和为
$$
D_k = \sum_{x_i \in C_k} \sum_{x_j \in C_k} \Vert x_i - x_j \Vert^2
$$
其中 $\Vert \cdot \Vert$ 为2范数。则对于聚类个数为 $K$ 时，我们可以定义一个测度量为
$$
W_K = \sum_{k=1}^K \frac{1}{2n_k} D_k
$$
对于不同的 $K$，经过 K-means 算法后我们会得到不同的中心点和数据点所属的簇，从而得到不同的度量 $W_K$。将聚类个数 $K$ 作为横坐标，$W_K$ 作为纵坐标，我们可以得到类似下面的图像：

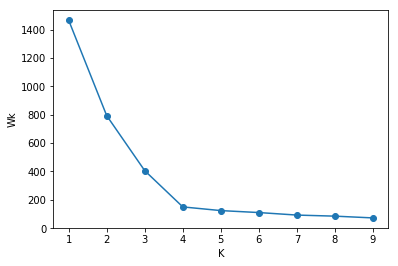
图像中图形很像人的手肘，该方法的命名就是从这而来。从图像中我们可以观察到，$K = 1$ 到 $4$ 下降很快，$K = 4$ 之后趋于平稳，因此 $K = 4$ 是一个拐点，手肘法认为这个拐点就是最佳的聚类个数 $K$。

手肘法是一个经验方法，观察结果因人而异，特别是遇到拐点位置不是很明显时。相比于前面的观察法，该方法的优点在于其适用于高维度的数据。

Trick

如果每个簇的中心点为该簇中的所有数据点的平均值时，即
$$
\mu_k = \frac{1}{n_k} \sum_{x_i \in C_k} x_i
$$
则 $D_k$ 可以写为
$$
D_k = \sum_{x_i \in C_k} \sum_{x_j \in C_k} \Vert x_i - x_j \Vert^2 = 2n_k \sum_{x_i \in C_k} \Vert x_i - \mu_k \Vert^2
$$
$W_K$ 写为
$$
W_K = \sum_{k=1}^K \frac{1}{2n_k} D_k = \sum_{k=1}^K \sum_{x_i \in C_k} \Vert x_i - \mu_k \Vert^2
$$

Note: 以下为公式推导内容，可略过。将 $D_k$ 表达式分解可得：
$$
\begin{align}
& \sum_{x_i \in C_k} \sum_{x_j \in C_k} \Vert x_i - x_j \Vert^2 \
= & \sum_{x_i \in C_k} \sum_{x_j \in C_k} \Vert (x_i - \mu_k) - (x_j - \mu_k) \Vert^2 \
= & \sum_{x_i \in C_k} \sum_{x_j \in C_k} \left( \Vert x_i - \mu_k \Vert^2 + \Vert x_j - \mu_k \Vert^2 - 2 \left< x_i - \mu_k, x_j - \mu_k \right> \right) \
= & \sum_{x_i \in C_k} n_k \Vert x_i - \mu_k \Vert^2 + \sum_{x_j \in C_k} n_k \Vert x_j - \mu_k \Vert^2 - 2 \sum_{x_i \in C_k} \sum_{x_j \in C_k} \left< x_i - \mu_k, x_j - \mu_k \right> \
= & 2 \sum_{x_i \in C_k} n_k \Vert x_i - \mu_k \Vert^2 - 2 \sum_{x_i \in C_k} \sum_{x_j \in C_k} \left< x_i - \mu_k, x_j - \mu_k \right>
\end{align}
$$
其中
$$
\begin{align}
& \sum_{x_i \in C_k} \sum_{x_j \in C_k} \left< x_i - \mu_k, x_j - \mu_k \right> \
= & \sum_{x_i \in C_k} \left< x_i - \mu_k, \sum_{x_j \in C_k} (x_j - \mu_k) \right>
\end{align}
$$
由于
$$
\sum_{x_j \in C_k} (x_j - \mu_k) = \sum_{x_j \in C_k} x_j - n_k \mu_k = ; n_k \mu_k - n_k \mu_k = 0
$$
则
$$
\sum_{x_i \in C_k} \sum_{x_j \in C_k} \left< x_i - \mu_k, x_j - \mu_k \right> = 0
$$
因此可以得到
$$
\sum_{x_i \in C_k} \sum_{x_j \in C_k} \Vert x_i - x_j \Vert^2 = 2 n_k \sum_{x_i \in C_k} \Vert x_i - \mu_k \Vert^2
$$

Gap Statistic方法

这个方法来源于论文[3]，详细内容可以去阅读该论文。延用前面关于度量 $W_K$ 的计算方式，该算法的流程如下：

cluster the observed data, varying the total number of clusters from $K=1, 2, \ldots, K_{\text{max}}$, and giving within-dispersion measures $W_K, K=1, 2, \ldots, K_{\text{max}}$
generate $B$ reference data sets and cluster each one giving within-dispersion measures $W_{Kb}$, $b=1,2, \ldots, B$, $K=1, 2, \ldots, K_{\text{max}}$. Compute the gap statistic
$$
\text{Gap}(K) =\frac{1}{B} \sum_{b=1}^B \log(W_{Kb}) - \log(W_K)
$$
let $\bar{w} = \frac{1}{B} \sum_{b=1}^B \log(W_{Kb})$, compute the standard deviation
$$
\text{sd}K = \left[ \frac{1}{B} \sum{b=1}^B (\log(W_{Kb}) - \bar{w})^2 \right]^{\frac{1}{2}}
$$
and define $s_K = \text{sd}_K \sqrt{1 + \frac{1}{B}}$
choose the number of clusters as the smallest $K$ such that $\text{Gap(K)} \ge \text{Gap(K+1)} - s_{K+1}$

关于 reference data sets 的生成，论文给了两种生成方法，这里只用其中一个，即对于生成的样本 $x_r$，其维度为 $d$，该样本的元素 $x_{ri}$ 的值按照均匀分布 $U(a, b)$ 随机生成，其中 $a$ 为待聚类的所有数据点的第 $i$ 位置元素的最小值， $b$ 为数据点的第 $i$ 位置元素的最大值。经过实验发现，这个算法的 3，4 步骤可以去掉，只用第 2 步计算出的 $\text{Gap}(K)$，然后选择最大 $\text{Gap}(K)$ 所对应的 $K$ 作为最优的聚类个数。这里贴出从一个数据集中得到的 $\text{Gap}(K)$ 的变化曲线图

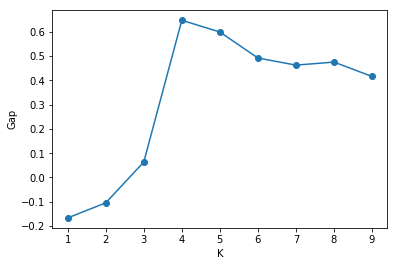
可以发现，当 $K = 4$ 时，$\text{Gap}(K)$ 取得最大值，因此选择 $K = 4$ 作为最优的聚类个数。该算法实现的代码为：

import numpy as np


def calculate_Wk(data, centroids, cluster):
    K = centroids.shape[0]
    wk = 0.0
    for k in range(K):
        data_in_cluster = data[cluster == k, :]
        center = centroids[k, :]
        num_points = data_in_cluster.shape[0]
        for i in range(num_points):
            wk = wk + np.linalg.norm(data_in_cluster[i, :]-center, ord=2) ** 2

    return wk


def bounding_box(data):
    dim = data.shape[1]
    boxes = []
    for i in range(dim):
        data_min = np.amin(data[:, i])
        data_max = np.amax(data[:, i])
        boxes.append((data_min, data_max))

    return boxes


def gap_statistic(data, max_K, B, cluster_algorithm):
    num_points, dim = data.shape
    K_range = np.arange(1, max_K, dtype=int)
    num_K = len(K_range)
    boxes = bounding_box(data)
    data_generate = np.zeros((num_points, dim))

    ''' 写法1
    log_Wks = np.zeros(num_K)
    gaps = np.zeros(num_K)
    sks = np.zeros(num_K)
    for ind_K, K in enumerate(K_range):
        cluster_centers, labels, _ = cluster_algorithm(data, K)
        log_Wks[ind_K] = np.log(calculate_Wk(data, cluster_centers, labels))

        # generate B reference data sets
        log_Wkbs = np.zeros(B)
        for b in range(B):
            for i in range(num_points):
                for j in range(dim):
                    data_generate[i][j] = \
                        np.random.uniform(boxes[j][0], boxes[j][1])
            cluster_centers, labels, _ = cluster_algorithm(data_generate, K)
            log_Wkbs[b] = \
                np.log(calculate_Wk(data_generate, cluster_centers, labels))
        gaps[ind_K] = np.mean(log_Wkbs) - log_Wks[ind_K]
        sks[ind_K] = np.std(log_Wkbs) * np.sqrt(1 + 1.0 / B)
    '''

    ''' 写法2
    '''
    log_Wks = np.zeros(num_K)
    for indK, K in enumerate(K_range):
        cluster_centers, labels, _ = cluster_algorithm(data, K)
        log_Wks[indK] = np.log(calculate_Wk(data, cluster_centers, labels))

    gaps = np.zeros(num_K)
    sks = np.zeros(num_K)
    log_Wkbs = np.zeros((B, num_K))

    # generate B reference data sets
    for b in range(B):
        for i in range(num_points):
            for j in range(dim):
                data_generate[i, j] = \
                    np.random.uniform(boxes[j][0], boxes[j][1])
        for indK, K in enumerate(K_range):
            cluster_centers, labels, _ = cluster_algorithm(data_generate, K)
            log_Wkbs[b, indK] = \
                np.log(calculate_Wk(data_generate, cluster_centers, labels))

    for k in range(num_K):
        gaps[k] = np.mean(log_Wkbs[:, k]) - log_Wks[k]
        sks[k] = np.std(log_Wkbs[:, k]) * np.sqrt(1 + 1.0 / B)

    return gaps, sks, log_Wks

参考

K-means怎么选K?
k-means的k值该如何确定？
Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2001, 63(2): 411-423.